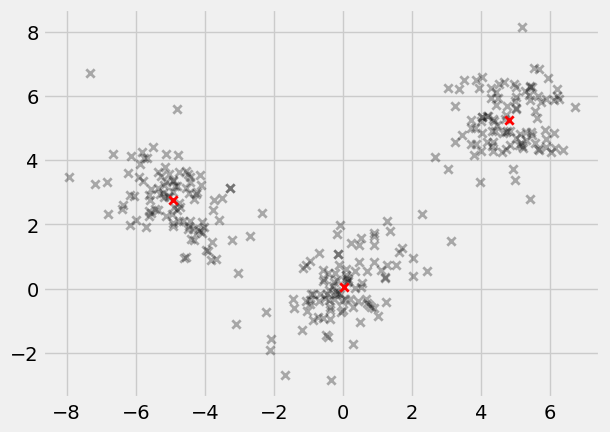
Naive k-means
This short post introduces the well-known naive k-means algorithm, a proof of its convergence, and an implementation in NumPy.
Within-cluster sum of squares (WCSS)
Consider partitioning points in Euclidean space such that “nearby” points are in the same subset. To measure the quality of such a partition, we need an objective function mapping each partition to a number. The within-cluster sum of squares (WCSS) is one such possible choice of objective.
Formally, given a finite dimensional subset $\mathcal{X}$ of Euclidean space, the WCSS of a partition $\Pi$ of these points is
\[\operatorname{WCSS}(\Pi)\equiv \sum_{\pi \in \Pi} \sum_{x \in \pi} \left\Vert x - \mathbb{E} X_\pi \right\Vert^2\]where $X_{\pi}\sim\operatorname{Uniform}(\pi)$ so that $\mathbb{E} X_\pi$ is the mean of the partition $\pi$.
Naive k-means
Naive k-means is an algorithm that attempts to optimize WCSS over all partitions of size $k$. While not guaranteed to optimize WCSS, it is guaranteed to converge to a local minimum.
The algorithm is iterative: given a partition $\Pi$, the next partition $\Pi^{\prime}$ is produced by reassigning each observation to its nearest mean. Formally,
\[\Pi^{\prime}=\left\{ \left\{ x\in\mathcal{X}\colon\tau(x)=\pi\right\} \colon\pi\in\Pi\right\}\]where
\[\tau(x)\in\operatorname{argmin}_{\pi\in\Pi}\left\Vert x-\mathbb{E}X_{\pi}\right\Vert ^{2}.\]Proposition. The k-means algorithm converges (i.e., $\Pi^\prime = \Pi$) after a finite number of steps.
Proof. To establish convergence of k-means, it is sufficient to prove that each iteration produces an improvement: $\operatorname{WCSS}(\Pi^{\prime})\leq\operatorname{WCSS}(\Pi)$. Since the WCSS is bounded below by zero and there are only finitely many partitions, the result follows. Indeed,
\[\begin{align*} \operatorname{WCSS}(\Pi) & =\sum_{\pi\in\Pi}\sum_{x\in\pi}\left\Vert x-\mathbb{E}X_{\pi}\right\Vert ^{2}\\ & \geq\sum_{\pi\in\Pi}\sum_{x\in\pi}\left\Vert x-\mathbb{E}X_{\tau(x)}\right\Vert ^{2}\\ & =\sum_{\pi\in\Pi^{\prime}}\sum_{x\in\pi}\left\Vert x-\mathbb{E}X_{\tau(x)}\right\Vert ^{2}\\ & \geq\sum_{\pi\in\Pi^{\prime}}\min_{c\in\mathbb{R}^{p}}\sum_{x\in\pi}\left\Vert x-c\right\Vert ^{2}\\ & =\sum_{\pi\in\Pi^{\prime}}\sum_{x\in\pi}\left\Vert x-\mathbb{E}X_{\pi}\right\Vert ^{2}\\ & =\operatorname{WCSS}(\Pi^{\prime}). \blacksquare \end{align*}\]Implementation
Below is an implementation of the algorithm.
The initial partition is constructed by sampling $k$ points $x_1, \ldots, x_k$ (without replacement) from $\mathcal{X}$. Each point in $\mathcal{X}$ is then assigned to the closest of $x_1, \ldots, x_k$. This choice of initialization, while easy to code, can produce poor results (e.g., consider the case in which all $k$ points are picked close to one another). The reader interested in improving initialization is referred to k-means++.
from typing import NamedTuple
import numpy as np
from numpy.typing import NDArray
class KMeansResult(NamedTuple):
"""Result of running k-means.
Attributes
----------
centroids
Array of shape (n_clusters, n_features)
converged
Whether or not the algorithm converged or was terminated early
n_iters
Number of iterations
"""
centroids: NDArray
converged: bool
n_iters: int
def k_means(
data: NDArray,
n_clusters: int,
generator: np.random.Generator | None = None,
max_iters: int = 1000,
tolerance: float = 1e-3,
) -> KMeansResult:
"""Runs k-means.
Parameters
----------
data
Array of shape (n_samples, n_features)
n_clusters
Number of clusters
generator
Random generator (if unspecified, `np.random.default_rng()` is used)
max_iters
Maximum number of iterations before giving up
tolerance
Convergence tolerance threshold
Returns
-------
KMeansResult object
"""
n, _ = data.shape
k = n_clusters
if n < k:
msg = f"The number of points ({n}) should be at least as large as the number of centroids ({k})"
raise RuntimeError(msg)
if generator is None:
generator = np.random.default_rng()
def init_centroids(n_points: int) -> NDArray:
# TODO: Improve by using k-means++ initialization
return data[generator.choice(n, size=(n_points,), replace=False)]
centroids = init_centroids(k) # (k, p)
prev_centroids = np.full_like(centroids, np.nan)
n_iters = 0
converged = False
while n_iters < max_iters:
if converged := ((centroids - prev_centroids) ** 2).mean() <= tolerance:
break
# For each point, find the closest centroid
squared_dists = ((data[:, np.newaxis, :] - centroids) ** 2).sum(axis=-1)
closest = np.argmin(squared_dists, axis=-1)
# Update centroids
prev_centroids = centroids
centroids = np.stack([data[closest == i].mean(axis=0) for i in range(k)])
# If a centroid has no points, re-initialize it
mask = np.any(np.isnan(centroids), axis=-1)
centroids[mask] = init_centroids(mask.sum())
n_iters += 1
return KMeansResult(centroids=centroids, converged=converged, n_iters=n_iters + 1)
Converged in 6 iterations