Parsiad Azimzadeh

Principal component analysis - part two

Introduction

In the first post in this series, we outlined the motivation and theory behind principal component analysis (PCA), which takes points $x_1, \ldots, x_N$ in a high dimensional space to points in a lower dimensional space while preserving as much of the original variance as possible.

In this follow-up post, we apply principal components regression (PCR), an algorithm which includes PCA as a subroutine, to a small dataset to demonstrate the ideas in practice.

Prerequisites

To understand this post, you will need to be familiar with the following concepts:

Ordinary least squares

In ordinary least squares (OLS), we want to find a line of best fit between the points $x_1, \ldots, x_N$ and the labels $y_1, \ldots, y_N$.

Denoting by $X$ the matrix whose rows are the points and $y$ the vector whose entries are the labels, the intercept $\alpha$ and slope (a.k.a. gradient) $\beta$ are obtained by minimizing $\Vert \alpha + X \beta - y \Vert$. Some matrix calculus reveals that the minimum is obtained at the values of $\alpha$ and $\beta$ for which

\[N \alpha = y^\intercal e - \beta^\intercal X^\intercal e\]

and

\[X^\intercal X \beta = X^\intercal y - \alpha X^\intercal e\]

where $e$ is the vector of all ones.

Principal components regression

The idea behind PCR is simple: instead of doing OLS on the high dimensional space, we first map the points to a lower dimensional space obtained by PCA and then do OLS. In more detail, we

  1. pick a positive integer $k < p$,
  2. construct the matrix $V_k$ whose columns are the first $k$ principal components of $X$,
  3. compute $Z_k = X V_k$, a matrix whose rows are the original points transformed to a lower dimensional “PCA space”, and
  4. perform OLS to find a line of best fit between the transformed points and $y$.

By the previous section, we know that the minimum is obtained at the values of the intercept $\alpha_k$ and gradient $\beta_k$ for which

\[N \alpha_k = y^\intercal e - \beta_k^\intercal Z_k^\intercal e\]

and

\[Z_k^\intercal Z_k \beta_k = Z_k^\intercal y - \alpha_k Z_k^\intercal e\]

Once we have solved these equations for $\alpha_k$ and $\beta_k$, we can predict the label $\hat{y}$ corresponding to a new sample $x$ as $\hat{y} = \alpha_k + x^\intercal V_k \beta_k$.

Computational considerations

Due to the result below, the linear system involving $\alpha_k$ and $\beta_k$ is a (permuted) arrowhead matrix. As such, the system can be solved efficiently.

Lemma. $Z_k^\intercal Z_k = \Sigma_k^2$ where $\Sigma_k$ is the $k \times k$ diagonal matrix whose entries are the first $k$ principal components of $X$ in descending order.

Proof. Let $v_j$ denote the $j$-th column of $V_k$. Since $v_j$ is a principal component of $X$, it is also an eigenvector of $X^\intercal X$ with eigenvalue $\sigma_j^2$, the square of the $j$-th singular value. Therefore, the $(i, j)$-th entry of $Z_k^\intercal Z_k$ is

\[(X v_i)^\intercal (X v_j) = v_i^\intercal X^\intercal X v_j = \sigma_j^2 v_i^\intercal v_j = \sigma_j^2 \delta_{ij}.\]

where $\delta_{ij}$ is the Kronecker delta.

The California housing dataset

The California housing dataset from [1] has 20,640 samples and 8 predictors. Below, we load it and split it into training and test sets.

np.random.seed(1)
X_all, y_all = fetch_california_housing(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X_all, y_all, test_size=0.2)

PCR

A PCR model takes only a few lines to create in scikit-learn:

pcr = make_pipeline(
    StandardScaler(),
    PCA(),
    LinearRegression(),
)
pcr.fit(X_train, y_train)

Pipeline(steps=[('standardscaler', StandardScaler()), ('pca', PCA()),
                ('linearregression', LinearRegression())])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

For each $k \leq p = 8$, we report the root mean squared error (RMSE) on both the training and test sets. The function used to do this is given in the Appendix accompanying this article.

Rank (k) Training set RMSE (in $100,000s) Test set RMSE (in $100,000s)
1 1.15492 1.14608
2 1.14128 1.12491
3 1.13947 1.12457
4 0.853976 0.844071
5 0.853972 0.844123
6 0.810381 0.807466
7 0.729905 0.731179
8 0.723369 0.72742

Both training and test set RMSEs are (roughly) decreasing functions of the rank. This suggests that using all 8 predictors does not cause overfitting.

Polynomial PCR

One way to reduce the test set RMSE is to capture nonlinear interactions between features.

Consider, as a toy example, a dataset where each sample $x_i$ has only three predictors: $x_i \equiv (a_i, b_i, c_i)$. We can replace each sample $x_i$ by a new sample $x_i^\prime \equiv (a_i, b_i, c_i, a_i^2, a_i b_i, a_i c_i, b_i^2, b_i c_i, c_i^2)$. In particular, we have added all possible quadratic monomials in $a_i, b_i, c_i$. We refer to these as derived predictors as they are predictors derived from the original features. Note that derived predictors need not be quadratic, or even monomials; any function of the original predictors is referred to as a derived predictor.

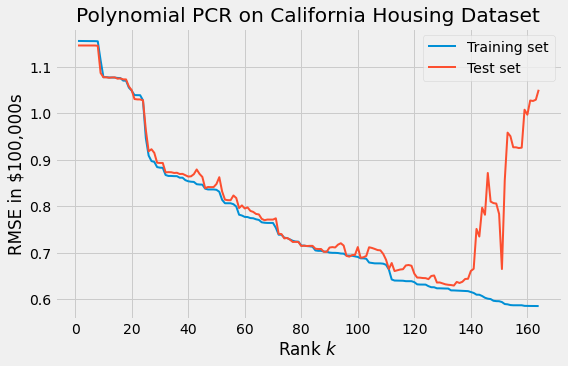
Returning to the dataset, we add all cubic monomials. It is reasonable to expect that unlike OLS applied to $X$, OLS applied to the derived matrix $X^\prime$ will overfit. We plot the results of PCR below, observing the effects of overfitting at large values of the rank.

polynomial_pcr = make_pipeline(
    StandardScaler(),
    PolynomialFeatures(degree=3, include_bias=False),
    PCA(),
    LinearRegression(),
)
polynomial_pcr.fit(X_train, y_train)

Pipeline(steps=[('standardscaler', StandardScaler()),
                ('polynomialfeatures',
                 PolynomialFeatures(degree=3, include_bias=False)),
                ('pca', PCA()), ('linearregression', LinearRegression())])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

png

Radial basis function PCR

Radial basis functions (RBFs) are another way to generate derived predictors. Unlike polynomial features, radial basis functions are more well-behaved: they typically do not suffer from the catastrophic overfitting seen in the previous section. While describing RBFs is out of the scope of this article, we show the results of RBF PCR below.

scaler = StandardScaler()
rbf = make_pipeline(
    scaler,
    RBFSampler(gamma=1.0, n_components=1_000, random_state=42)
)
union = FeatureUnion([
    ("original_features", scaler),
    ("rbf_features", rbf),
])
rbf_pcr = make_pipeline(
    union,
    PCA(),
    LinearRegression(),
)
rbf_pcr.fit(X_train, y_train)

Pipeline(steps=[('featureunion',
                 FeatureUnion(transformer_list=[('original_features',
                                                 StandardScaler()),
                                                ('rbf_features',
                                                 Pipeline(steps=[('standardscaler',
                                                                  StandardScaler()),
                                                                 ('rbfsampler',
                                                                  RBFSampler(n_components=1000,
                                                                             random_state=42))]))])),
                ('pca', PCA()), ('linearregression', LinearRegression())])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

png

Bibliography

[1] Pace, R. Kelley, and Ronald Barry. “Sparse spatial autoregressions.” Statistics & Probability Letters 33.3 (1997): 291-297.

Appendix: Function to compute PCR model RMSE

def get_rmses(pipeline: Pipeline, train: bool) -> NDArray:
    """Calculates the RMSE of a model using only the first k PCs for each possible value of k.

    Parameters
    ----------
    pipeline
        An sklearn `Pipeline` whose last two components are `PCA` and `LinearRegression`
    train
        Whether to calculate the RMSE on the train or test set

    Returns
    -------
    A list of RMSEs (the first entry corresponds to k=1 and the last to k=p).
    """
    X, y = (X_train, y_train) if train else (X_test, y_test)
    assert isinstance(pipeline[-2], PCA)
    assert isinstance(pipeline[-1], LinearRegression)
    pca = pipeline[:-1]
    Z = pca.transform(X)
    regression = pipeline[-1]
    rmses = np.empty((Z.shape[1],))
    for k in range(1, Z.shape[1] + 1):
        pred = regression.intercept_ + Z[:, :k] @ regression.coef_[:k]
        rmse = (mean_squared_error(y, pred))**0.5
        rmses[k - 1] = rmse
    return rmses