mlinterp

mlinterp is a fast C++ routine for linear interpolation in arbitrary dimensions (i.e., multilinear interpolation).
mlinterp is written by Parsiad Azimzadeh and released under a permissive MIT License. The latest release can be downloaded here.
👷 Including mlinterp in your project
Method 1: Quick and dirty
mlinterp is a header-only library, meaning that the quickest (albeit dirtiest) way to get started is to copy the file mlinterp/mlinterp.hpp into your own project directory and include it using #include "mlinterp.hpp".
Method 2: Git submodule (preferred)
If you are working on a Git project, adding mlinterp as a submodule is preferred. Doing so makes it easy to distribute your code and pick up new versions of mlinterp when they are released.
If you are unfamiliar with submodules, you can read about them in the online Git documentation.
Method 3: System-wide install
Run the following commands (from the mlinterp project directory) to install it to your system:
cmake .
sudo make install
You can now include it using #include <mlinterp>.
🧑🏫 Examples
1d
Let’s interpolate y = sin(x) on the interval [-pi, pi] using 15 evenly-spaced data points.
using namespace mlinterp;
// Boundaries of the interval [-pi, pi]
constexpr double b = 3.14159265358979323846, a = -b;
// Subdivide the interval [-pi, pi] using 15 evenly-spaced points and
// evaluate sin(x) at each of those points
constexpr int nxd = 15, nd[] = { nxd };
double xd[nxd];
double yd[nxd];
for(int n = 0; n < nxd; ++n) {
xd[n] = a + (b - a) / (nxd - 1) * n;
yd[n] = sin(xd[n]);
}
// Subdivide the interval [-pi, pi] using 100 evenly-spaced points
// (these are the points at which we interpolate)
constexpr int ni = 100;
double xi[ni];
for(int n = 0; n < ni; ++n) {
xi[n] = a + (b - a) / (ni - 1) * n;
}
// Perform the interpolation
double yi[ni]; // Result is stored in this buffer
interp(
nd, ni, // Number of points
yd, yi, // Output axis (y)
xd, xi // Input axis (x)
);
// Print the interpolated values
cout << scientific << setprecision(8) << showpos;
for(int n = 0; n < ni; ++n) {
cout << xi[n] << "\t" << yi[n] << endl;
}
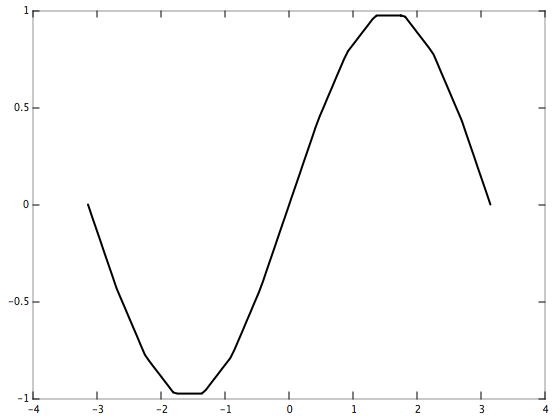
Note that the points do not have to be evenly spaced. Try modifying the above to use a non-uniform grid!
2d
Let’s interpolate z = sin(x)cos(y) on the interval [-pi, pi] X [-pi, pi] using 15 evenly-spaced points along the x axis and 15 evenly-spaced points along the y axis.
using namespace mlinterp;
// Boundaries of the interval [-pi, pi]
constexpr double b = 3.14159265358979323846, a = -b;
// Discretize the set [-pi, pi] X [-pi, pi] using 15 evenly-spaced
// points along the x axis and 15 evenly-spaced points along the y axis
// and evaluate sin(x)cos(y) at each of those points
constexpr int nxd = 15, nyd = 15, nd[] = { nxd, nyd };
double xd[nxd];
for(int i = 0; i < nxd; ++i) {
xd[i] = a + (b - a) / (nxd - 1) * i;
}
double yd[nyd];
for(int j = 0; j < nyd; ++j) {
yd[j] = a + (b - a) / (nyd - 1) * j;
}
double zd[nxd * nyd];
for(int i = 0; i < nxd; ++i) {
for(int j = 0; j < nyd; ++j) {
const int n = j + i * nyd;
zd[n] = sin(xd[i]) * cos(yd[j]);
}
}
// Subdivide the set [-pi, pi] X [-pi, pi] using 100 evenly-spaced
// points along the x axis and 100 evenly-spaced points along the y axis
// (these are the points at which we interpolate)
constexpr int m = 100, ni = m * m;
double xi[ni];
double yi[ni];
for(int i = 0; i < m; ++i) {
for(int j = 0; j < m; ++j) {
const int n = j + i * m;
xi[n] = a + (b - a) / (m - 1) * i;
yi[n] = a + (b - a) / (m - 1) * j;
}
}
// Perform the interpolation
double zi[ni]; // Result is stored in this buffer
interp(
nd, ni, // Number of points
zd, zi, // Output axis (z)
xd, xi, yd, yi // Input axes (x and y)
);
// Print the interpolated values
cout << scientific << setprecision(8) << showpos;
for(int n = 0; n < ni; ++n) {
cout << xi[n] << "\t" << yi[n] << "\t" << zi[n] << endl;
}
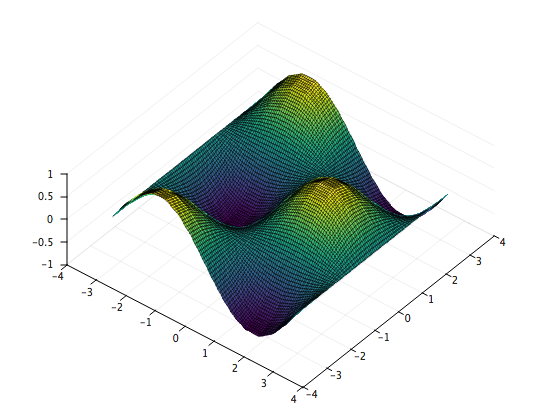
Note that the x and y axes do not have to be identical: they can each have any number of unequally spaced points. Try modifying the above to use different x and y axes!
Higher dimensions (3d, 4d, …)
In general, if you have k dimensions with axes x1, x2, …, xk, the interp routine is called as follows:
interp(
nd, ni, // Number of points
yd, yi, // Output axis
x1d, x1i, x2d, x2i, ..., xkd, xki // Input axes
);
🦸 Advanced
Orders
In the 2d example, the interp routine assumes that the array zd is “ordered” in a certain way.
In particular, if i is the index associated with the x axis and j is the index associated with the y axis, n = j + i * nyd gives the index of the corresponding element in the zd array.
This is referred to as the natural order, and it generalizes to arbitrary dimensions. If instead we wanted n = i + j * nxd, we would use the reverse natural order, which can be invoked by using instead
interp<rnatord>(nd, ni, zd, zi, xd, xi, yd, yi);
You are free to define your own ordering scheme. To get a sense of how to do this, it’s easiest to study the code for the natural order:
struct natord {
template <typename Index, Index Dimension>
static Index mux(const Index *nd, const Index *indices) {
Index index = 0, product = 1, i = Dimension - 1;
while(true) {
index += indices[i] * product;
if(i == 0) { break; }
product *= nd[i--];
}
return index;
}
};
