mlinterp - Fast arbitrary dimension linear interpolation in C++
I made a header-only C++ library for arbitrary dimension linear interpolation (a.k.a. multilinear interpolation). The design philosophy is to push as much to compile-time as possible by template metaprogramming.
Instructions for how to include it in your work are on the GitHub project page.
Below are some simple examples of its usage.
Examples
1d
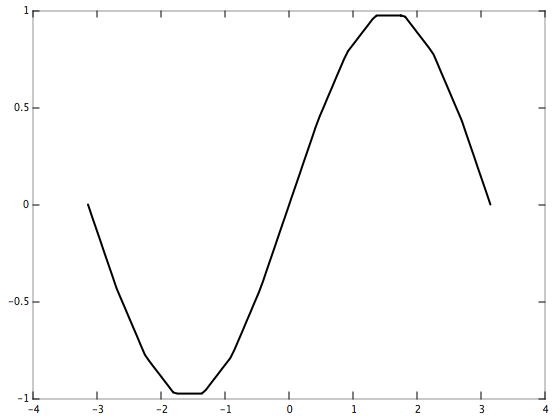
Let’s interpolate y = sin(x) on the interval [-pi, pi] using 15 evenly-spaced data points.
using namespace mlinterp;
// Boundaries of the interval [-pi, pi]
constexpr double b = 3.14159265358979323846, a = -b;
// Subdivide the interval [-pi, pi] using 15 evenly-spaced points and
// evaluate sin(x) at each of those points
constexpr int nxd = 15, nd[] = { nxd };
double xd[nxd];
double yd[nxd];
for(int n = 0; n < nxd; ++n) {
xd[n] = a + (b - a) / (nxd - 1) * n;
yd[n] = sin(xd[n]);
}
// Subdivide the interval [-pi, pi] using 100 evenly-spaced points
// (these are the points at which we interpolate)
constexpr int ni = 100;
double xi[ni];
for(int n = 0; n < ni; ++n) {
xi[n] = a + (b - a) / (ni - 1) * n;
}
// Perform the interpolation
double yi[ni]; // Result is stored in this buffer
interp(
nd, ni, // Number of points
yd, yi, // Output axis (y)
xd, xi // Input axis (x)
);
// Print the interpolated values
cout << scientific << setprecision(8) << showpos;
for(int n = 0; n < ni; ++n) {
cout << xi[n] << "\t" << yi[n] << endl;
}
Note that the points do not have to be evenly spaced. Try modifying the above to use a non-uniform grid!
2d
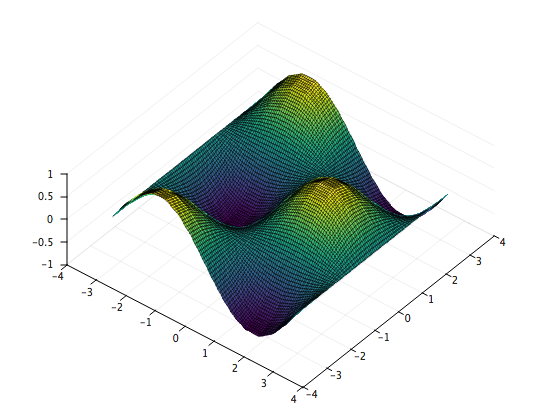
Let’s interpolate z = sin(x)cos(y) on the interval [-pi, pi] X [-pi, pi] using 15 evenly-spaced points along the x axis and 15 evenly-spaced points along the y axis.
using namespace mlinterp;
// Boundaries of the interval [-pi, pi]
constexpr double b = 3.14159265358979323846, a = -b;
// Discretize the set [-pi, pi] X [-pi, pi] using 15 evenly-spaced
// points along the x axis and 15 evenly-spaced points along the y axis
// and evaluate sin(x)cos(y) at each of those points
constexpr int nxd = 15, nyd = 15, nd[] = { nxd, nyd };
double xd[nxd];
for(int i = 0; i < nxd; ++i) {
xd[i] = a + (b - a) / (nxd - 1) * i;
}
double yd[nyd];
for(int j = 0; j < nyd; ++j) {
yd[j] = a + (b - a) / (nyd - 1) * j;
}
double zd[nxd * nyd];
for(int i = 0; i < nxd; ++i) {
for(int j = 0; j < nyd; ++j) {
const int n = j + i * nyd;
zd[n] = sin(xd[i]) * cos(yd[j]);
}
}
// Subdivide the set [-pi, pi] X [-pi, pi] using 100 evenly-spaced
// points along the x axis and 100 evenly-spaced points along the y axis
// (these are the points at which we interpolate)
constexpr int m = 100, ni = m * m;
double xi[ni];
double yi[ni];
for(int i = 0; i < m; ++i) {
for(int j = 0; j < m; ++j) {
const int n = j + i * m;
xi[n] = a + (b - a) / (m - 1) * i;
yi[n] = a + (b - a) / (m - 1) * j;
}
}
// Perform the interpolation
double zi[ni]; // Result is stored in this buffer
interp(
nd, ni, // Number of points
zd, zi, // Output axis (z)
xd, xi, yd, yi // Input axes (x and y)
);
// Print the interpolated values
cout << scientific << setprecision(8) << showpos;
for(int n = 0; n < ni; ++n) {
cout << xi[n] << "\t" << yi[n] << "\t" << zi[n] << endl;
}
Note that the x and y axes do not have to be identical: they can each have any number of unequally spaced points. Try modifying the above to use different x and y axes!
Higher dimensions (3d, 4d, …)
In general, if you have k dimensions with axes x1, x2, …, xk, the interp routine is called as follows:
interp(
nd, ni, // Number of points
yd, yi, // Output axis
x1d, x1i, x2d, x2i, ..., xkd, xki // Input axes
);