Closed-form expressions for perpetual and finite-maturity American binary options

Abstract. In this article, we derive an analytic formula for the value of American binary (a.k.a. digital) put and call options under Black-Scholes model of option pricing. This model includes the assumption that the underlying asset follows a geometric Brownian motion. The availability of an analytic formula gives practitioners easy access to options pricing Greeks for hedging and sensitivity analyses. We handle the general case in which a finite expiry time ($T < \infty$) is specified for the option, obtaining formulas for the perpetual ($T = \infty$) case by taking limits. Our approach is as follows: we first show that the option value is identical to the Laplace transform of $f \cdot \chi_{[0, T]}$ evaluated at the risk free rate of return where $f$ is the density of the first time an arithmetic Brownian motion hits a particular level. We then derive an expression for the Laplace transform using ordinary calculus. The expression for the Laplace transform may be of independent interest. We verify the correctness of the expression using both symbolic algebra and numerical PDEs.

Updated August 10, 2024. A previous version of this article defined the symbol $a$ (see below) erroneously. Namely, it was defined as the negation of the quantity that now appears in the corrected article. Thanks to Grant Garrison for catching this error.

American binary option

A binary option is a type of option in which pays off either some fixed amount (e.g., one dollar) or nothing at all.

An American binary put pays the holder exactly one dollar if the asset on which it is written drops below a specific valuation, called the strike. For example, consider owning an American binary put with a strike price of 100 dollars, expiring in a year, and written on AAPL stock (which, for the purposes of this example, we assume trades at some value of greater than 100 dollars today). If at any point in time between now and a year from now AAPL stock drops below 100 dollars, we will receive one dollar by exercising the option.

An American binary call is similar, except that it pays the holder exactly one dollar if the asset on which it is written goes above a specific valuation.

Mathematical formulation

We assume that, under the pricing measure, the price of the stock (e.g., APPL) at time $t$ is given by

\[S_t = S_0 \exp\biggl( \left(r - \delta - \frac{1}{2} \sigma^2 \right) t + \sigma W_t \biggr)\]

where the initial price $S_0$ and volatility $\sigma$ are positive, the interest rate $r$ is real, and the dividend rate $\delta$ is nonnegative. $W$ is a standard Wiener process.

Let $K$ denote the (nonnegative) strike price. If $S_0 \leq K$, the American binary put should be exercised immediately and is thus worth exactly one dollar. We call this the trivial case. Analogously, if $S_0 \geq K$, the American binary call is worth one dollar. Therefore, we proceed assuming the nontrivial case (i.e., $S_0 > K$ for puts and $S_0 < K$ for calls).

Let $\tau$ be the first time the asset hits level $K$. It follows that, for each realization, $\tau$ is either infinite or satisfies

\[\log S_0 + \left( r - \delta - \frac{1}{2} \sigma^2 \right) \tau + \sigma W_\tau = \log K.\]

We can rewrite the above equation as $\mu \tau + W_\tau = a$ where

\[\mu = \frac{r - \delta - \frac{1}{2} \sigma^2}{\sigma} \quad \text{and} \quad a = \frac{\log K - \log S_0}{\sigma}.\]

In other words, $\tau$ is the first time a Wiener process with drift $\mu$ (a.k.a. an arithmetic Brownian motion) hits the level $a$. The density of the first time a Wiener process with drift $\mu$ hits the level $a$ is well-known:

\[f(t) = \frac{\left| a \right|}{\sqrt{2 \pi t^3}} \exp \biggl( -\frac{\left( a - \mu t \right)^2}{2t} \biggr).\]

Next, let $T \leq \infty$ be the expiry time of the option. Since the option should be exercised as soon as it is in the money (i.e., at time $\tau$), it follows that the fair price of either instrument (in the nontrivial case) is

\[\mathbb{E} e^{-r \tau} \chi_{[0, T]}(\tau) = \int_0^T e^{-r t} f(t) dt\]

where $\chi_A$ is the indicator function on a set $A$. The notation above reveals that this is none other than the Laplace transform of $f \cdot \chi_{[0, T]}$ evaluated at $r$.

Lemma. $\mu^2 + 2r$ is nonnegative.

Proof. If $r$ is nonnegative, the result is trivial. If $r$ is negative, then since $\delta$ is nonnegative,

\[\left( \mu^2 + 2r \right) \sigma^2 \geq \left(r - \frac{1}{2} \sigma^2 \right)^2 + 2r \sigma^2 = r^2 + r \sigma^2 + \frac{1}{4} \sigma^4 = \left(r + \frac{1}{2} \sigma^2 \right)^2 \geq 0.\quad \blacksquare\]

Laplace transform

In this section, we give an expression for the Laplace transform. We do not assume particular forms for $a$ and $\mu$. Below, we use $\Phi(\cdot)$ and $\operatorname{sgn}(\cdot)$ to denote the normal cumulative distribution function and signum function, respectively.

Theorem. Let $\mu$, $a$, and $r$ be real numbers and $T$ be positive. Let $\tau$ be the first time a Wiener process with drift $\mu$ hits the level $a$. If $b \equiv \sqrt{\mu^2 + 2r}$ is real, then

\[% = \frac{1}{2} e^{a (\mu - b)} \left( % 1 % + \operatorname{sgn}(a) \operatorname{erf}\biggl(\frac{bT - a}{\sqrt{2T}}\biggr) % + e^{2ab} \left( % 1 % - \operatorname{sgn}(a) \operatorname{erf}\biggl(\frac{bT + a}{\sqrt{2T}}\biggr) % \right) % \right) % = \frac{1}{2} e^{a (\mu - b)} \left( % \Phi \biggl( % \operatorname{sgn}(a) b \sqrt{T} - \frac{\left| a \right|}{\sqrt{T}} % \biggr) % + e^{2ab} \Phi \biggl( % -\operatorname{sgn}(a) b \sqrt{T} - \frac{\left| a \right|}{\sqrt{T}} % \biggr) % \right) \mathbb{E} e^{-r \tau} \chi_{[0, T]}(\tau) = e^{a (\mu - b)} \left[ \Phi \biggl( \operatorname{sgn}(a) \frac{b T - a}{\sqrt{T}} \biggr) + e^{2ab} \Phi \biggl( -\operatorname{sgn}(a) \frac{b T + a}{\sqrt{T}} \biggr) \right]\]

Proof. Denote by $F(T)$ the expression on the right-hand side of the above equation. Since $\operatorname{sgn}(a) a = |a|$ and

\[%\lim_{T \downarrow 0} \operatorname{erf} \biggl( \frac{bT \pm a}{\sqrt{2T}} \biggr) \lim_{T \downarrow 0} \Phi \biggl( \frac{\pm \operatorname{sgn}(a) b T - \left| a \right|}{\sqrt{T}} \biggr) = 0,\]

it follows that $\lim_{T \downarrow 0} F(T) = 0$.

If we can establish $F^\prime(t) = e^{-r t} f(t)$ for all $0 < t < \infty$, then by the fundamental theorem of calculus,

\[F(T) = F(T) - \lim_{t \downarrow 0} F(t) = \int_0^T e^{-r t} f(t) dt,\]

as desired. Indeed,

\[\begin{align*} F^{\prime}(t) & =\operatorname{sgn}(a)e^{a(\mu-b)}\left[\left(\frac{bt-a}{\sqrt{t}}\right)^{\prime}\varphi\biggl(\frac{bt-a}{\sqrt{t}}\biggr)-e^{2ab}\left(\frac{bt+a}{\sqrt{t}}\right)^{\prime}\varphi\biggl(\frac{bt+a}{\sqrt{t}}\biggr)\right]\\ & =\frac{\operatorname{sgn}(a)e^{a(\mu-b)}}{2\sqrt{2\pi t^{3}}}\left[\left(a+bt\right)\exp\biggl(-\frac{\left(a-bt\right)^{2}}{2t}\biggr)+e^{2ab}\left(a-bt\right)\exp\biggl(-\frac{\left(a+bt\right)^{2}}{2t}\biggr)\right]\\ & =\frac{\operatorname{sgn}(a)e^{a(\mu-b)}}{2\sqrt{2\pi t^{3}}}\left[\left(a+bt\right)\exp\biggl(-\frac{\left(a-bt\right)^{2}}{2t}\biggr)+\left(a-bt\right)\exp\biggl(-\frac{\left(a-bt\right)^{2}}{2t}\biggr)\right]\\ & =\frac{\left|a\right|e^{a(\mu-b)}}{\sqrt{2\pi t^{3}}}\exp\biggl(-\frac{\left(a-bt\right)^{2}}{2t}\biggr)\\ & =e^{-rt}\frac{\left|a\right|}{\sqrt{2\pi t^{3}}}\exp\biggl(-\frac{\left(a-\mu t\right)^{2}}{2t}\biggr). \quad \blacksquare \end{align*}\]

The infinite horizon case ($T = \infty$) follows immediately by taking limits as $T \rightarrow \infty$ and applying the dominated convergence theorem:

Corollary. If $b \equiv \sqrt{\mu^2 + 2r}$ is real, then $\mathbb{E} e^{-r \tau} = e^{a \mu - |a| b}$.

Implementation

import numpy as np
from numpy.typing import ArrayLike
from scipy.stats import norm

def american_binary(
    asset_price: ArrayLike,
    dividend_rate: ArrayLike,
    expiry_time: ArrayLike,
    risk_free_rate: ArrayLike,
    strike: ArrayLike,
    volatility: ArrayLike,
) -> ArrayLike:
    """Computes the value of an American binary option under the Black–Scholes model.

    If the asset price is less (resp., greater) than the strike price, the American binary put (resp., call) should be
    exercised immediately and is thus worth exactly one dollar.
    We call this the trivial case.
    This function computes only the nontrivial case, assuming the put (resp., call) value is desired when the price is
    greater (resp., less) than the strike price.

    Example
    -------
    >>> american_binary_put = american_binary(
    ...     asset_price=125.0,
    ...     strike=100.0,
    ...     risk_free_rate=0.04,
    ...     dividend_rate=0.01,
    ...     volatility=0.2,
    ...     expiry_time=1.0,
    ... )

    Parameters
    ----------
    asset_price
        The price of the asset at the initial time (S_0)
    dividend_rate
        The dividend rate (δ)
    expiry_time
        The option's time-to-expiry (T)
    risk_free_rate
        The risk-free rate of return (r)
    strike
        The strike price (K)
    volatility
        The volatility (σ)

    Returns
    -------
    The value of an American binary put if the asset price is greater than the strike and the value of an American
    binary call otherwise
    """
    assert np.all(asset_price >= 0.)
    assert np.all(dividend_rate >= 0.)
    assert np.all(expiry_time >= 0.)
    assert np.all(strike >= 0.)
    assert np.all(volatility >= 0.)

    strike = np.maximum(strike, np.finfo(float).eps)
    asset_price = np.maximum(asset_price, np.finfo(float).eps)
    
    r = risk_free_rate
    T = expiry_time
    a = np.log(strike / asset_price) / volatility
    μ = (r - dividend_rate - 0.5 * volatility**2) / volatility
    b = np.sqrt(μ**2 + 2. * r)
    return np.exp(a * (μ - b)) * (
        norm.cdf(np.sign(a) * (b * T - a) / np.sqrt(T))
        + np.exp(2. * a * b) * norm.cdf(-np.sign(a) * (b * T + a) / np.sqrt(T))
    )

png

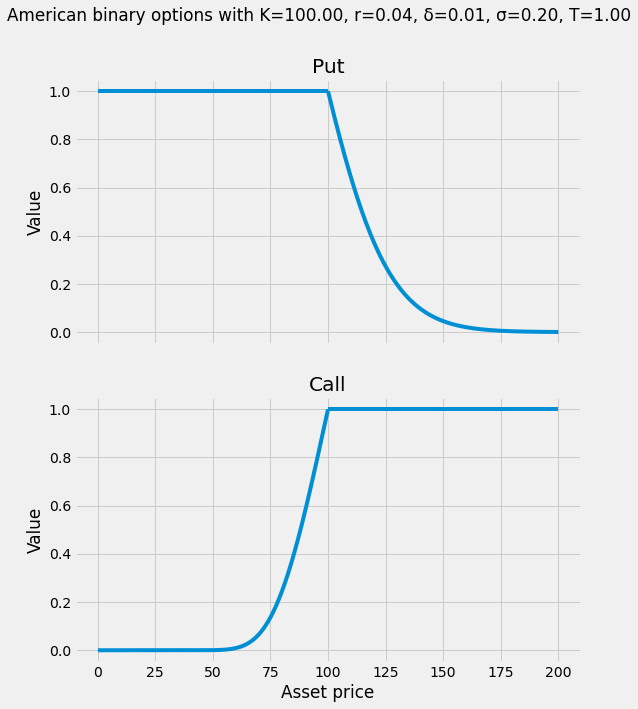
Appendix

In this appendix, we validate the identity both symbolically (via SageMath) and numerically (via numerical PDE methods).

Symbolic validation

Below, we use SageMath to verify that $F^\prime(t) = e^{-rt} f(t)$.

var("t a r μ")
assume(t > 0)
assume(a, "real")
assume(r, "real")
assume(μ, "real")
b = sqrt(μ^2 + 2 * r)
F = 1/2 * exp(a * (μ - b)) * (
    1 + sign(a) * erf((b * t - a) / sqrt(2 * t)) + exp(2 * a * b) * (
        1 - sign(a) * erf((b * t + a) / sqrt(2 * t))))
f = sign(a) * a / sqrt(2 * pi * t^3) * exp(- (a - μ * t)^2 / (2 * t))
delta = diff(F, t) - exp(-r * t) * f
assert delta.canonicalize_radical() == 0

Numerical PDE validation

Let $V(t, S_t)$ be the value of the American binary put at time $t$ with asset price $S_t \geq K$. By standard dynamic programming arguments, the function $V: [0, T] \times \Omega \rightarrow \mathbb{R}$ where $\Omega = (K, \infty)$ is a solution of the following boundary value problem (BVP):

\[\begin{align*} \frac{\partial V}{\partial t}+\frac{1}{2}\sigma^{2}S^{2}\frac{\partial^{2}V}{\partial S^{2}}+\left(r-\delta\right)S\frac{\partial V}{\partial S}-rV & =0 & \text{on }[0,T)\times\Omega\\ V & =1 & \text{on }[0,T]\times\{K\}\\ V & =0 & \text{ on }\{T\}\times\Omega. \end{align*}\]

The value of the American binary call with asset price $S_t \leq K$ satisfies the same BVP but with the domain replaced by $\Omega = [0, K)$.

Below, a finite difference solver for the BVP is given. The solver quantizes time and space. At each point in quantized time, it solves a tridiagonal linear system using the Thomas algorithm. Tables generated from this code, also given below, demonstrate that as the quantization is made finer, the error between the numeric and analytic solutions vanish.

import numpy as np
from numba import njit
from numpy.typing import NDArray

@njit
def solve_tridiag(a: NDArray, b: NDArray, c: NDArray, d: NDArray) -> NDArray:
    """Solves a tridiagonal linear system using the Thomas algorithm.

    Parameters
    ----------
    a: ndarray of shape (n - 1,)
        Subdiagonal
    b: ndarray of shape (n,)
        Diagonal
    c: ndarray of shape (n - 1,)
        Superdiagonal
    d: ndarray of shape (n,)
        Right hand side

    Returns
    -------
    x: ndarray of shape (n,)
        Solution
    """
    n = d.size

    c_new = np.empty_like(a)
    d_new = np.empty_like(d)
    
    c_new[0] = c[0] / b[0]
    d_new[0] = d[0] / b[0]
    
    for i in range(1, n - 1):
        denom = b[i] - a[i - 1] * c_new[i - 1]
        c_new[i] = c[i] / denom
        d_new[i] = (d[i] - a[i - 1] * d_new[i - 1]) / denom
    
    d_new[n - 1] = (d[n - 1] - a[n - 2] * d_new[n - 2]) / (b[n - 1] - a[n - 2] * c_new[n - 2])

    x = np.empty_like(d)
    x[n - 1] = d_new[n - 1]
    
    for i in range(n-2, -1, -1):
        x[i] = d_new[i] - c_new[i] * x[i+1]
    
    return x

def american_binary_pde(
    dividend_rate: float,
    expiry_time: float,
    risk_free_rate: float,
    strike: float,
    volatility: float,
    put: bool = True,
    num_points: int = 10_000,
    num_steps: int = 10_000,
) -> tuple[NDArray, NDArray]:
    """Computes the value of an American binary option via a numerical PDE method.

    Parameters
    ----------
    put
        Whether to compute the value of an American binary put or call
    num_points
        Number of asset price grid points
    num_steps
        Number of time steps to take

    Returns
    -------
    S
        Grid of asset prices
    V
        Value of option on the grid at the initial time
    """
    δ, T, r, K, σ = dividend_rate, expiry_time, risk_free_rate, strike, volatility
    
    # When solving the call option, use a grid on [0, K]
    # When solving the put, use a grid on [K, H] where H is chosen large enough
    H = np.exp(np.log(K) - (r - δ - 0.5 * σ**2) * T + 7.0 * σ * T**0.5)
    S = np.linspace(K if put else 0., H if put else K, num_points + 1)
    
    # Since the coefficients of the PDE are constant in time, the matrix
    # in the linear system solved at each timestep is also constant
    Δt = T / num_steps
    Sn = np.concatenate(((np.nan,), S[:-1]))
    Sp = np.concatenate((S[1:], (np.nan,)))
    ΔSn = S - Sn
    ΔSp = Sp - S
    wn = +2.0 / (ΔSn * (ΔSn + ΔSp))
    w  = -2.0 / (ΔSn * ΔSp)
    wp = +2.0 / (ΔSp * (ΔSn + ΔSp))
    a =              - 0.5 * σ**2 * S**2 * Δt * wn
    b = 1.0 + r * Δt - 0.5 * σ**2 * S**2 * Δt * w
    c =              - 0.5 * σ**2 * S**2 * Δt * wp
    a = a[+1:]
    c = c[:-1]
    a[-1] = c[0] = 0.
    b[0] = b[-1] = 1.
    
    # Solution vector
    V = np.zeros((num_points + 1,))
    V[0 if put else -1] = 1.0  # Exercise boundary
    
    # Average value of the asset after one timestep
    S_next = (1.0 + (r - δ) * Δt) * S
    
    for n in range(num_steps - 1, -1, -1):
        V_next = np.interp(S_next, S, V)
        V_next[-1 if put else +0] = 0.0
        V_next[+0 if put else -1] = 1.0  # Exercise boundary
        V = solve_tridiag(a, b, c, V_next)

    return S, V

Put

	K	r	δ	σ	T	num_points	num_steps	L2 error	L∞ error
0	100.0	0.04	0.01	0.2	1.0	100	100	0.049058	0.004720
1	100.0	0.04	0.01	0.2	1.0	200	200	0.016633	0.002290
2	100.0	0.04	0.01	0.2	1.0	400	400	0.005757	0.001129
3	100.0	0.04	0.01	0.2	1.0	800	800	0.002014	0.000560
4	100.0	0.04	0.01	0.2	1.0	1600	1600	0.000708	0.000279
5	100.0	0.04	0.01	0.2	1.0	3200	3200	0.000250	0.000139
6	100.0	0.04	0.01	0.2	1.0	6400	6400	0.000088	0.000070
7	100.0	0.04	0.01	0.2	1.0	12800	12800	0.000031	0.000035

Call

	K	r	δ	σ	T	num_points	num_steps	L2 error	L∞ error
0	100.0	0.04	0.01	0.2	1.0	100	100	0.003907	0.000985
1	100.0	0.04	0.01	0.2	1.0	200	200	0.001333	0.000476
2	100.0	0.04	0.01	0.2	1.0	400	400	0.000463	0.000234
3	100.0	0.04	0.01	0.2	1.0	800	800	0.000162	0.000116
4	100.0	0.04	0.01	0.2	1.0	1600	1600	0.000057	0.000058
5	100.0	0.04	0.01	0.2	1.0	3200	3200	0.000020	0.000029
6	100.0	0.04	0.01	0.2	1.0	6400	6400	0.000007	0.000014
7	100.0	0.04	0.01	0.2	1.0	12800	12800	0.000003	0.000007

Parsiad Azimzadeh